Fat-Tailed Distributions and Black Swan Events: Why They Matter

The concepts of fat-tailed distributions and black swan events, as popularized by Nassim Nicholas Taleb in seminal work "The Black Swan: The Impact of the Highly Improbable" (2007), have indeed become critical for understanding risk and uncertainty in various fields, including finance and drug development. Taleb's ideas challenge the traditional reliance on Gaussian distributions, which often underestimate the frequency and impact of rare, high-magnitude events. This is particularly relevant in contexts such as market crashes and unforeseen adverse effects in clinical trials, where conventional statistical models fail to account for the true nature of risks involved (Bratianu, 2020; Kjoersvik & Bate, 2022; Nafday, 2009).

This article delves into the fundamentals of fat-tailed distributions, their implications for drug development and diagnostics, and why accounting for them is essential for mitigating risk and unlocking opportunity.

Fundamentals of Fat Tails and Black Swans

What Are Fat-Tailed Distributions?

Fat-tailed distributions are characterized by their higher probabilities assigned to extreme outcomes compared to Gaussian distributions, where outliers are considered rare and their impacts diminish rapidly. This deviation is mathematically represented by a power-law relationship, indicating that as the magnitude of an event increases, its probability decreases at a slower rate than in Gaussian models. This characteristic is particularly evident in financial markets, where events like market crashes occur more frequently than traditional models would predict (Ma & Tanizaki, 2019; Takahashi et al., 2016; Jacquier et al., 2004). For instance, the 2008 financial crisis serves as a prime example of a black swan event, highlighting the inadequacies of standard risk assessment methods that rely on normal distribution assumptions (Kjoersvik & Bate, 2022; Nafday, 2009).

Mathematically, fat-tailed distributions often follow a power-law relationship:

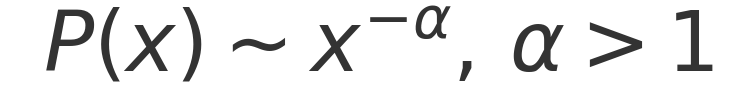
This implies that as event magnitudes increase, their probability decreases more slowly than in Gaussian distributions. In finance, for example, market crashes occur far more frequently than Gaussian models suggest.

The Power Law in Venture Capital and Medicine

Venture Capital

In venture capital, where a small number of investments yield disproportionately large returns. This phenomenon underscores the importance of recognizing high-risk, high-reward opportunities, as a single successful investment can offset numerous failures (Brugarolas et al., 2020; Adcock & Shutes, 2000). Similarly, in medicine, the implications of fat-tailed distributions are profound. For example, while a few drug therapies may revolutionize treatment paradigms, the majority fail to reach the market. Moreover, outliers in patient response data can provide critical insights for precision medicine, yet they are often overlooked due to the limitations of Gaussian assumptions (Aven, 2014).

Examples in Medicine

Power laws similarly govern breakthroughs and challenges in medicine:

• Drug Approvals: A few therapies revolutionize treatment paradigms, while most fail to reach the market.
• Diagnostics: Outliers in patient response data often hold the key to precision medicine but are overlooked under Gaussian assumptions.

What Are Sigma Levels?

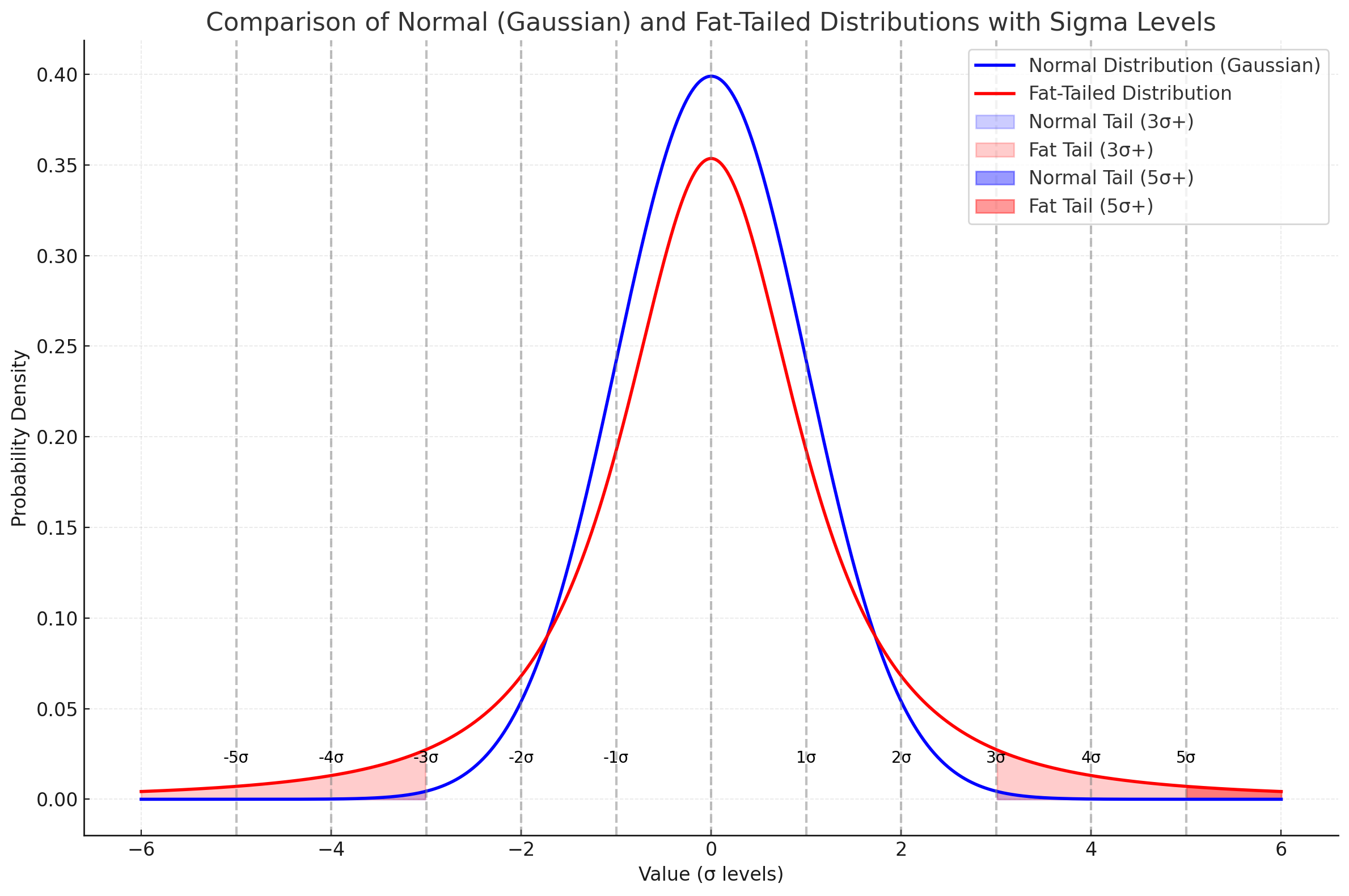
Sigma levels (σ), which measure standard deviations from the mean in a probability distribution, further illustrate the discrepancies between Gaussian and fat-tailed models. While Gaussian models predict that events beyond 3σ are exceedingly rare, fat-tailed distributions reveal that such events are, in fact, more common in practice. This has significant implications for both finance and drug development, where misjudging the likelihood of rare events can lead to catastrophic outcomes (Polasek, 2009; "Reviews", 2008).

Sigma levels measure the standard deviations from the mean in a probability distribution:

• 1σ 68.27% of data
• 2σ: 95.45% of data
• 3σ: 99.73% of data
• 5σ: 99.99994% of data (or a 1 in 3.5 million probability under Gaussian assumptions)

While Gaussian models predict that events beyond 3σ are exceedingly rare, fat-tailed distributions reveal these events to be far more common in practice.

Why Tail Events Matter

In Finance

1. Rare Events Aren’t Rare: Market crashes, such as the 2008 financial crisis, exemplify black swan events. Fat-tailed models better reflect the frequency and severity of such occurrences.
2. Misjudging Risk: Traditional portfolio management often underestimates extreme losses, resulting in unpreparedness for catastrophic financial shocks.

In Drug Development

1. Clinical Trial Outliers: Rare but severe adverse events can derail drug approval, especially in small subgroups of patients.
2. Efficacy Extremes: Exceptional responses in specific patients offer opportunities for breakthrough treatments but are often dismissed.
3. Regulatory Risks: Failing to account for tail events can lead to delayed approvals or post-market withdrawals, such as the thalidomide tragedy.

Case Study: Neurometry and Fat Tails

In drug development, the failure to account for tail events can result in severe consequences, such as the withdrawal of drugs from the market due to unforeseen adverse effects. Clinical trials often face challenges from rare but serious adverse events, which can derail approval processes, particularly in small patient subgroups. Furthermore, exceptional responses in specific patients can represent opportunities for breakthrough treatments, yet these are frequently dismissed under traditional statistical frameworks (Kjoersvik & Bate, 2022; Nafday, 2009; "Reviews", 2008). The case of neurometry (quantitative EEG) exemplifies these challenges, as the inherent fat-tailed properties of EEG signals can inflate false positives and distort diagnostic accuracy (Kjoersvik & Bate, 2022; "Reviews", 2008).

Neurometry (quantitative EEG or qEEG) relies on norm-based thresholds to diagnose abnormalities in brain activity. However, EEG signals inherently exhibit fat-tailed properties, leading to:

1. Inflation of False Positives: Monte Carlo simulations reveal that adopting a 3σ cut-off under fat-tailed assumptions (e.g., lognormal distributions) increases false positives by over 1,800%. This undermines diagnostic accuracy.
2. Spontaneous Recovery Issues: Fat-tailed distributions distort test-retest reliability, creating false confidence in diagnostic tools.
3. Transparency Concerns: Commercial qEEG providers rarely disclose the distributional properties of their datasets, perpetuating diagnostic inaccuracies.

Recommendations for Accounting for Fat Tails

For Diagnostics

1. Reevaluate Cut-Off Criteria: Replace Gaussian-based thresholds (e.g., 3σ) with models better suited to fat-tailed data, such as Bayesian frameworks.
2. Promote Data Transparency: Providers should disclose the properties of their datasets to enhance diagnostic accuracy.
3. Adopt Alternative Models: Use lognormal transformations or non-parametric approaches to minimize false positives.

For Drug Development

1. Integrate Fat-Tailed Models: Incorporate power-law or lognormal analyses into trial designs to anticipate extreme outcomes.
2. Focus on Tail Risks: Investors and regulators should prioritize rare-event modeling to mitigate unforeseen adverse effects.
3. Enhance Patient Stratification: Detailed analysis of outlier responses can optimize trial design and precision medicine efforts.

Broader Impacts and Conclusion

Fat-tailed distributions and black swan events highlight the limitations of traditional statistical models in capturing real-world complexity. By adopting models better suited to fat-tailed data, stakeholders can mitigate risks, anticipate extreme outcomes, and seize opportunities for breakthroughs. As Taleb emphasizes, embracing uncertainty transforms risk management into a proactive rather than reactive endeavor (Kjoersvik & Bate, 2022; Nafday, 2009; "Reviews", 2008).

References

(2008). Reviews. Significance, 5(1), 42-43. https://doi.org/10.1111/j.1740-9713.2008.00281.x

Adcock, C. and Shutes, K. (2000). Fat tails and the capital asset pricing model., 17-39. https://doi.org/10.1007/978-1-4615-4389-3_2

Aven, T. (2014). The concept of antifragility and its implications for the practice of risk analysis. Risk Analysis, 35(3), 476-483. https://doi.org/10.1111/risa.12279

Bratianu, C. (2020). A knowledge management approach to complex crises. Management Dynamics in the Knowledge Economy, 8(4), 345-356. https://doi.org/10.2478/mdke-2020-0022

Brugarolas, M., Martínez, L., Rabadán, A., & Cañete, R. (2020). Innovation strategies of the spanish agri-food sector in response to the black swan covid-19 pandemic. Foods, 9(12), 1821. https://doi.org/10.3390/foods9121821

Jacquier, É., Polson, N., & Rossi, P. (2004). Bayesian analysis of stochastic volatility models with fat-tails and correlated errors. Journal of Econometrics, 122(1), 185-212. https://doi.org/10.1016/j.jeconom.2003.09.001

Kjoersvik, O. and Bate, A. (2022). Black swan events and intelligent automation for routine safety surveillance. Drug Safety, 45(5), 419-427. https://doi.org/10.1007/s40264-022-01169-0

Ma, D. and Tanizaki, H. (2019). Fat-tailed stochastic volatility model and the stock market returns in china. China Finance Review International, 11(2), 170-184. https://doi.org/10.1108/cfri-03-2018-0028

Nafday, A. (2009). Strategies for managing the consequences of black swan events. Leadership and Management in Engineering, 9(4), 191-197. https://doi.org/10.1061/(asce)lm.1943-5630.0000036

Polasek, W. (2009). Nassim nicholas taleb: the black swan: the impact of the highly improbable. Statistical Papers, 52(1), 247-249. https://doi.org/10.1007/s00362-009-0226-8

Takahashi, M., Watanabe, T., & Omori, Y. (2016). Volatility and quantile forecasts by realized stochastic volatility models with generalized hyperbolic distribution. International Journal of Forecasting, 32(2), 437-457. https://doi.org/10.1016/j.ijforecast.2015.07.005